Es un blog de sencillas y prácticas clases de matemática para estudiantes de secundaria.
lunes, 18 de noviembre de 2013
miércoles, 6 de noviembre de 2013
Binomio de Newton y Triángulo de Pascal
Recuerdan el trabajo que les dejé sobre el Triángulo de Pascal, veamos su relación con el Binomio de Newton.
. La factorización de polinomios como un juego.
Al estudiar la factorización es interesante verla también gráficamente; en el siguiente video verás algo interesante.....no te vayas a aburrir....miralo atentamente ....en realidad es interesante... te va a gustar.....
viernes, 2 de agosto de 2013
Como Hacer un Cubo de Papel
Les pedí en clase a mis alumnas hacer un cubo de papel sin usar pegamento solo, papel,y tijeras, algunas de ellas lograron hacerlo, con unas ideas muy ingeniosas, y las que quedaron con la tarea para el día siguiente, me presentaron su cubo siguiendo los diseños de los siguientes videos
Veamos ahora algunas fotos de mis alumnas haciendo sus cubos.
domingo, 28 de julio de 2013
Trucos matemáticos: ¿Cómo multiplicar sin volverte loco?
El matemático Rob Eastway le explica a la BBC que no se trata de memorizar, sino de revelar los secretos de los números

Ir más allá de la tabla del 10 también tiene algo de juego.
No se trata de aprender a memorizar, sino de disfrutar de la profusión de patrones que se revelan cuando aprendemos a multiplicar, asegura el escritor y matemático Rob Eastaway.
Hubo una época, hace varias décadas, en la que muchos niños del mundo tenían una razón obvia para aprenderse la tabla del 12. Todos los países que usaban las medidas imperiales británicas calculaban en pies y pulgadas y pagaban en chelines y peniques.
Multiplicar por 12 era una experiencia cotidiana.
Pero eso es historia antigua, aunque los huevos aún se venden en docenas, y mucha gente -incluidos los estadounidenses- todavía midan en pulgadas.
Nada de eso justifica pasar horas repitiendo esas tablas extra.
Y sin embargo, sigue habiendo una razón para aprenderse “la del doce”. Algo que tiene más que ver con el descubrimiento de patrones y con tener confianza al manejar números.
Apenas los niños se empiezan a sentir cómodos multiplicando números más grandes que 10, comienzan a entender las multiplicaciones largas.
Saberse las tablas del 11 y del 12 puede introducir patrones intrigantes de los que podrían perderse si paran en la del 10.
LO DIVERTIDO DEL 11
Mucho de la tabla de multiplicar por 11 es fácil de aprender: 2 × 11 es 22, 8 veces 11 es 88. Y cuando uno pasa de 12, hay patrones simpáticos para descubrir.
Mucho de la tabla de multiplicar por 11 es fácil de aprender: 2 × 11 es 22, 8 veces 11 es 88. Y cuando uno pasa de 12, hay patrones simpáticos para descubrir.
¿Quieres multiplicar 11 × 23? Simplemente tome los dos dígitos -2 y 3-, súmalos (da 5) y pon ese número en la mitad: 253. ¡Tadaaaa!
¿Qué tal 36 × 11? De nuevo, separa el 3 del 6 y ponga su suma en la mitad: 396. Maravilloso.
¡Pero cuidado! Si los dos dígitos suman más de 9, este genial truco no funciona tan bien.
58 × 11… pues 5 + 8 = 13, pero la respuesta no es 5138. Ese “1” del 13 realmente representa a un 10, por lo que tiene que ser añadido al 5 para que dé la respuesta correcta: 638.
Hay otro patrón que empieza con 11 × 11.
Multiplique esos dos número y le da 121.
¿Y 111 × 111? La respuesta es 12321.
¿Puede adivinar cuánto es 1111 × 1111? 1234321.
EL 12
Multiplicar por 12, por su lado, es más simple cuando uno se da cuenta de que es lo mismo que multiplicar un número por 10 y añadir el doble del primer número.
Multiplicar por 12, por su lado, es más simple cuando uno se da cuenta de que es lo mismo que multiplicar un número por 10 y añadir el doble del primer número.
Entonces, 12 × 12 es 10 × 12 (=120), y luego se le añade 2 × 12 (=24), lo que da 120 + 24 = 144.
Esa regla no se limita a la tabla de multiplicar, que se suspendería en 12 × 12.
12 × 61 es lo mismo que 10 × 61 (=610) más 2 × 61 (=122) y si puede sumar 610 + 122 en su mente, tendrá la respuesta correcta: 732.
¿Es necesario memorizar la respuesta de 12 × 12? Realmente no. Mientras se acuerde de la estrategia para hacer los cálculos, llegará a la respuesta con casi la misma rapidez.
Pero claro, al hacerlo a menudo, se queda en la memoria, lo que agiliza el proceso en esos momentos en los que necesita un resultado pronto.
¿SEGUIR HASTA 20?
¿Por qué parar en la tabla del 12? Se podría seguir con la del 13, 14… hasta la del 20, como se hace en algunos países.
¿Por qué parar en la tabla del 12? Se podría seguir con la del 13, 14… hasta la del 20, como se hace en algunos países.
Lo que pasa es que si uno entiende las tablas de multiplicar básicas hasta el 10, tiene las herramientas necesarias para llegar al resultado de, digamos, 19 × 14.
Y si uno pasa demasiado tiempo memorizando las respuestas a esas preguntas, no va a tener tiempo para entender cómo funcionan los números.
De lo que realmente se tratan las matemáticas es de entender patrones y resolver problemas.
Rob Eastaway es coautor del libro “Matemáticas para mamás y papás”
Etiquetas:
matematica es un juego,
multiplicaciones,
multiplicar,
trucos matemáticos
domingo, 16 de junio de 2013
PROYECTO DE INVESTIGACIÓN: POLINOMIOS
 He obtenido éste proyecto del libro Hipervínculos de Santillana, y vamos a elaborarlos como inicio de la unidad de Polinomios.
He obtenido éste proyecto del libro Hipervínculos de Santillana, y vamos a elaborarlos como inicio de la unidad de Polinomios.Los Depósitos de Gas
El Perú posee una de las mayores reservas recuperables de gas natural de América del Sur, en los lotes 56 y 58 de Camisea. Los inmensos volúmenes que se extraen de éste gas, constituido principalmente por metano, requieren de instalación de depósitos especiales para su almacenamiento y de una red de ductos para el transporte por tierra y por mar.
Los enormes tanques que contienen éste gas y las tuberías por donde pasa tienen forma de sólidos geométricos, cuyo volumen puede expresarse en función del radio o longitud de las bases y altura. Esto se representa mediante expresiones algebraicas, donde el volumen de las áreas de los sólidos ( cilindro, prisma,...) toman valores numéricos según los valores que se den a las variables de las que dependen.
Realizaremos la siguiente investigación
1. Investiguen cuáles son las expresiones algebraicas que representan el área lateral, el área total y el volumen del prisma y el cilindro.
2.Calculen el volumen de los cuerpos mencionados si cada una de las variables tomara el valor de un metro.¿Han utilizado el número real PI en éstos cálculos?¿En que casos?¿El valor de Pi es variable o es constante?
Explica.
3. Establezca la diferencia entre la división de polinomios y la división de números enteros. Visiten las páginas web
http://www.authorstream.com/Presentation/Juanjoexpo-146589-el-lenguaje-algebraico-para-stream-education-ppt-powerpoint/
http://www.camisea.com.pe/esp/project.asp.
4 Investiguen la ubicación de Camisea, el volumen estimado de la producción de gas y el destino de los hidrocarburos extraídos en los lotes 56 y 88
5. En grupos realizamos lo siguiente:
Comparamos lo que hemos investigado
Explicamos las semejanzas que existen entre la división de polinomios y la división de números enteros
Anotamos las conclusiones finales.
.
.
lunes, 10 de junio de 2013
¿Porque estamos tan Mal en Matemáticas?
Encontré éste artículo en la Web, me parece tan interesante que decidí compartirlo con Uds
El artículo.nos habla de las diferentes razones por las cuales estamos tan mal en matemática; y tiene como punto de partida la evaluación Censal 2012 en el área de Matemáticas en la provincia de Canchis, Región Cuzco.
Los resultados, causas y pautas para evitar el fracaso son similares en todas las regiones; el fracaso en las matemáticas no es solo por culpa de uno de los actores en el proceso de aprendizaje, todos tenemos algo de responsabilidad en ello y debemos asumir el compromiso que nos corresponde de acuerdo al rol que desempeñamos, sea el de estudiante, padre de familia o profesor.
Podemos ademas señalar que hasta el número de alumnos por aula es un indicador que nos lleva al fracaso en el área; también es la falta de capacitación para los profesores, estamos en una etapa de cambio, y debemos comprometernos a ello.
Lee el artículo y asume el compromiso de cambiar para que los resultados sean mas alentadores.
El artículo.nos habla de las diferentes razones por las cuales estamos tan mal en matemática; y tiene como punto de partida la evaluación Censal 2012 en el área de Matemáticas en la provincia de Canchis, Región Cuzco.
Los resultados, causas y pautas para evitar el fracaso son similares en todas las regiones; el fracaso en las matemáticas no es solo por culpa de uno de los actores en el proceso de aprendizaje, todos tenemos algo de responsabilidad en ello y debemos asumir el compromiso que nos corresponde de acuerdo al rol que desempeñamos, sea el de estudiante, padre de familia o profesor.
Podemos ademas señalar que hasta el número de alumnos por aula es un indicador que nos lleva al fracaso en el área; también es la falta de capacitación para los profesores, estamos en una etapa de cambio, y debemos comprometernos a ello.
Lee el artículo y asume el compromiso de cambiar para que los resultados sean mas alentadores.
miércoles, 22 de mayo de 2013
PROYECTO EDUCATIIVO
Vamos a realizar un proyecto educativo de Operaciones con Números Reales; en la parte inferior encontrarás las indicaciones del proyecto,
lunes, 29 de abril de 2013
LA RAÍZ MORTAL
Hace mucho que no publico nada pero, hoy leyendo algo sobre la historia de los números irracionales, encontré el nombre de HIPASO y su muerte fue lo que me intrigó, asi que busqué y encontré este artículo de gaussianos.com que comparto con Uds.
La muerte de Hipaso
La historia que vamos a contar se desarrolla en torno al siglo V a.C. en la antigua Grecia y los protagonistas son los pitagóricos. Esta secta de matemáticos/filósofos (huelga decir que en aquella época matemático y filósofo era prácticamente lo mismo) era muy peculiar, tanto en lo que se refiere a sus creencias como en lo que se refiere a sus costumbres. Podemos decir que su figura principal es Pitágoras, aunque en realidad no se sabe a ciencia cierta si este personaje existió en realidad.
Hemos dicho que los protagonistas de la historia que nos ocupa son los pitagóricos, pero en realidad el protagonista principal es, por razones que veremos más adelante, uno de ellos: Hipaso de Metaponto.
Los pitagóricos tenían la firme creencia que todo el Universo podía ser explicado con números. Pero, ¿con qué números? Pues con números naturales, esto es, 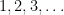 , y con las fracciones que pueden formarse con ellos, es decir,
, y con las fracciones que pueden formarse con ellos, es decir,  . En cierto modo puede ser una creencia lícita y hasta cierto punto razonable (recordemos que estamos en la antigua Grecia), pero que a la postre les salió rana.
. En cierto modo puede ser una creencia lícita y hasta cierto punto razonable (recordemos que estamos en la antigua Grecia), pero que a la postre les salió rana.
Y, según cuenta la leyenda, Hipaso fue el culpable (si se me permite utilizar este calificativo) de ello. Al parecer Hipaso se planteó el problema de medir la diagonal de un cuadrado utilizando el lado como unidad de medida. Por plantear el problema de la forma más simple posible, tomemos un cuadrado de lado  . En esta situación la pregunta que según parece se realizó Hipaso fue: ¿cuánto mide la diagonal de este cuadrado?
. En esta situación la pregunta que según parece se realizó Hipaso fue: ¿cuánto mide la diagonal de este cuadrado?

Teniendo en cuenta la condición de pitagórico de Hipaso, es posible que él mismo esperara que la medida de esta diagonal pudiera expresarse como un número natural o una fracción…pero en realidad no fue así. Hipaso se dio cuenta de que esta medida no podía expresarse ni como un número natural ni como una fracción formada por números naturales. Ahora sabemos que esta diagonal mide
Al menos esto cuenta la leyenda, esto es, que Hipaso fue el descubridor de este hecho. Lo que parece más cercano a la realidad fue que el propio Hipaso comunicó este descubrimiento fuera de la comunidad pitagórica…y esto fue lo que significó el final de Hipaso. Según algunas fuentes, los pitagóricos lo arrojaron al mar por revelar fuera de la secta esta catástrofe pitagórica, aunque otras aseguran que lo que hicieron los pitagóricos fue organizar un simulacro de funeral, con tumba incluida, que simbolizaba que para ellos Hipaso pasaba a estar muerto. Hasta se comenta que Hipaso podría haberse suicidado (hecho que podría cuadrar con la hipótesis del funeral simulado). Sea como fuere, la raíz de la muerte de Hipaso para lo pitagóricos, ya fuera ideológica o real, fue esa diagonal del cuadrado, ese número irracional, esa hecatombe pitagórica (¿cómo se iba a poder explicar el Universo con números naturales y fracciones si ni siquiera puede medirse la diagonal de un cuadrado con ellos?) que fue 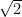 .
.
Suscribirse a:
Comentarios (Atom)


