Es un blog de sencillas y prácticas clases de matemática para estudiantes de secundaria.
miércoles, 24 de junio de 2015
domingo, 31 de mayo de 2015
Ecuación de la Recta: Punto-Pendiente
Forma punto-pendiente
La ecuación y = mx + n
que hemos visto se denomina forma explícita de la ecuación de la recta, y nos permite hallar dicha ecuación cuando conocemos la pendiente y la ordenada en el origen.
que hemos visto se denomina forma explícita de la ecuación de la recta, y nos permite hallar dicha ecuación cuando conocemos la pendiente y la ordenada en el origen.
Cuando sólo conocemos la pendiente, m, y las coordenadas de otro de los puntos de la recta, (xo,yo), su ecuación es
y - yo = m (x - xo)
Esta ecuación recibe el nombre de forma punto-pendiente de la ecuación de la recta. En el video se explica cómo se obtiene.Pendiente de una Recta, Teoría
En la ecuación principal de la recta
y = mx + b
el valor de
m corresponde a la pendiente de la recta
b es el coeficiente de posición o punto de intercepción con el eje de las ordenadas
La pendiente permite obtener el grado de inclinación que tiene una recta, mientras que el coeficiente de posición señala el punto en que la recta interceptará al eje de las ordenadas.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo que indica que interceptará al eje y en el punto (0,7).
Cuando se tienen dos puntos cualesquiera (x1,y1) y (x2,y2), la pendiente queda determinada por el cociente entre la diferencia de las ordenadas de dos puntos de ella y la diferencia de las abscisas de los mismos puntos, o sea
Observemos el video para clarificar los conceptos
APLICANDO LO APRENDIDO
Tenemos un grupo de problemas, con los cuales puedes practicar y ver tus avances en matemáticas, el texto tiene hipervínculos, que te llevarán alas páginas de éste blog que te brindarán ayuda para resolver los casos presentados.Espero que te sirva.
martes, 5 de mayo de 2015
Razones y proporciones ¿ que es una razon y una proporcion ?
Entender ¿Qué es una razón se te puede hacer difícil, pero observa éste video, es el mejor que he conseguido en la red
Ahora sí, podrás entender con mayor facilidad la siguiente situación significativa
Por mi cumpleaños recibí de regalo S/ 150 de los cuáles ahorré S/ 100, y mi hermana recibió S/ 120 y ahorró S/ 80 ¿Quién ahorró en mayor proporción?
Primero relacionamos las cantidades usando razones en su forma simplificada
 Ella ahorra S/ 80 soles de lo S/ 120 que recibe
Ella ahorra S/ 80 soles de lo S/ 120 que recibe
Ahora sí, podrás entender con mayor facilidad la siguiente situación significativa
Por mi cumpleaños recibí de regalo S/ 150 de los cuáles ahorré S/ 100, y mi hermana recibió S/ 120 y ahorró S/ 80 ¿Quién ahorró en mayor proporción?
Primero relacionamos las cantidades usando razones en su forma simplificada
Yo ahorro S/ 100 soles de los S/ 150 que recibo
100/ 150 = 2 / 3
La razón es : 2 de 3. Ahorré
S/ 2 soles por
cada S/ 3 que recibí.
Trabajamos ahora la razón para lo que ahorró mi hermana
80/ 120 = 2 / 3
La razón es : 2 de 3. Ahorró S/ 2 soles por
cada S/ 3 que recibió.
Tanto mi hermana como yo ahorramos S/ 2 soles de cada S/ 3 soles que recibimos.
Observamos que tanto mi hermana como yo ahorramos en la
misma proporción; es decir
100 / 150 es equivalente a 80 / 120 entonces 100 / 150 = 80 / 120 se lee: 100 es a 150 como 80 es a 120
Comprobaremos que las dos razones forman una proporción 100 / 150 = 80 / 120 entonces tenemos 100 x 120 = 150 x 80
El
producto de los extremos es igual al producto de los medios
Dadas dos razones
a / b y c / d
se llama proporción a la expresión a / b = c /d donde a x d = b x c
domingo, 3 de mayo de 2015
INTERÉS COMPUESTO
Recordemos la situación anterior de Alberto y su esposa solicitan un préstamo de S/ 18 000 a una TCEA de 12% por un período de 5 años lo trabajaremos al interés compuesto que es lo que cobran los bancos.
Muy bien ahora recuerda que en el Interés Compuesto; el Interés se reinvierte y llega a formar parte del capital, lo que significa que el Capital varía en cada período ( en éste caso en cada año), por lo que el interés también va a cambiar y será mayor cada período, pues se calcula de un monto mayor de capital.
Veamos como lo calculamos. como la tasa de interés es el 12 %, calculamos el interés a pagar el primer año
1 (18 000 x 12) / 100 = 2160 para el segundo año a éste interés le sumamos el capital inicial
2 18 000 + 2 160 = 20 160 y a éste resultado le sacamos el 12 % (20160 x 12 ) / 100 = 2 419,2 y repetimos. a éste resultado le sumamos el capital anterior.
3 20 160 + 2 419, 2 = 22 579,2 el interés sería ( 22 579,2 x 12 ) / 100 = 2 709, 50
4 22 579,2 + 2 709, 5 = 25 288, 7 el interés sería ( 25 288, 7 x 12) / 100 = 3 034, 64
y se va repitiendo hasta completar el período que te han solicitado, te darás cuenta que el monto a pagar será mucho mayor que el calculado anteriormente.
Existen fórmulas que harán mucho mas sencillo éstos cálculos ya las veremos mas adelante en clase.
Muy bien ahora recuerda que en el Interés Compuesto; el Interés se reinvierte y llega a formar parte del capital, lo que significa que el Capital varía en cada período ( en éste caso en cada año), por lo que el interés también va a cambiar y será mayor cada período, pues se calcula de un monto mayor de capital.
Veamos como lo calculamos. como la tasa de interés es el 12 %, calculamos el interés a pagar el primer año
1 (18 000 x 12) / 100 = 2160 para el segundo año a éste interés le sumamos el capital inicial
2 18 000 + 2 160 = 20 160 y a éste resultado le sacamos el 12 % (20160 x 12 ) / 100 = 2 419,2 y repetimos. a éste resultado le sumamos el capital anterior.
3 20 160 + 2 419, 2 = 22 579,2 el interés sería ( 22 579,2 x 12 ) / 100 = 2 709, 50
4 22 579,2 + 2 709, 5 = 25 288, 7 el interés sería ( 25 288, 7 x 12) / 100 = 3 034, 64
y se va repitiendo hasta completar el período que te han solicitado, te darás cuenta que el monto a pagar será mucho mayor que el calculado anteriormente.
Existen fórmulas que harán mucho mas sencillo éstos cálculos ya las veremos mas adelante en clase.
|
AÑOS
|
1
|
2
|
3
|
4
|
5
|
...
|
15
|
total
|
|
Interés (12%)
|
2160
|
2419,2
|
2709,5
|
3034,64
|
|
|
|
|
|
Capital Inicial
|
|
|
||||||
|
Capital Final (Monto)
|
|
|
||||||
INTERÉS SIMPLE
Si es muy difícil para tí comprender como se saca el interés simple; iremos paso a paso.Trabajaremos con una situación significativa:
 Alberto y su esposa cuentan con una casa propia . Su propiedad, ubicada en el distrito de Miraflores, está a medio construir . Les falta terminar el primer piso, los acabados y quieren levantar un segundo nivel. Para ello han pensado en un préstamo, el que financiarán hipotecando el mismo inmueble .
Alberto y su esposa cuentan con una casa propia . Su propiedad, ubicada en el distrito de Miraflores, está a medio construir . Les falta terminar el primer piso, los acabados y quieren levantar un segundo nivel. Para ello han pensado en un préstamo, el que financiarán hipotecando el mismo inmueble .
Pero debemos tener en cuenta que los bancos te cobran con un interés compuesto y además cobran tasas y comisiones, por lo que es importante conocer la TCEA que cobran, eso lo vemos en la siguiente entrada.
 Alberto y su esposa cuentan con una casa propia . Su propiedad, ubicada en el distrito de Miraflores, está a medio construir . Les falta terminar el primer piso, los acabados y quieren levantar un segundo nivel. Para ello han pensado en un préstamo, el que financiarán hipotecando el mismo inmueble .
Alberto y su esposa cuentan con una casa propia . Su propiedad, ubicada en el distrito de Miraflores, está a medio construir . Les falta terminar el primer piso, los acabados y quieren levantar un segundo nivel. Para ello han pensado en un préstamo, el que financiarán hipotecando el mismo inmueble .
En la región y el país, diferentes bancos otorgan préstamos hipotecarios. Estos créditos son pagaderos en más de 10 años, su tasa de interés es preferencial (menos del 15% anual) y se deja como prenda la propiedad que se compra o mejora .
Supongamos que Alberto y su esposa piden un préstamo S/ 18 000 a una tasa de interés de 12 % anual ¿Cuánto pagará de interés después de 15 años?
Primero trabajaremos como si el banco les cobra con Interés Simple
Qué es lo que necesitas conocer para sacar el interés Simple?
Pues Debes conocer :
el Capital ( en éste caso el dinero que pides en préstamo S/ 18 000)
La tasa de interés ( 12 % anual)
el Tiempo (15 años)
también debes recordar que en el Interés Simple el capital Inicial no varía, que el interés que pagas siempre será el mismo por que no se reinvierte y porque se calcula del mismo capital.
Existen diferentes maneras de sacar el interés Simple, lo haremos lo mas sencillo para que entiendas
Como el capital es de 18 000 calcularemos su 12 %, podemos usar la regla de tres simple:
(18 000 x 12 ) / 100 y obtendremos 2160 que representa el interés anual que pagarán;
como ellos van a pagarlo en 15 años lo multiplicamos por 15 es decir 2160 x 15 = 32 400 que es lo que pagarían de intereses Alberto y su esposa por los 15 años.
al finalizar los 15 años el total a pagar sería el Capital Inicial que les prestaron ( 18 000 ) mas los intereses generados ( 32 400), es decir terminaría pagando S/ 50 400.
como ellos van a pagarlo en 15 años lo multiplicamos por 15 es decir 2160 x 15 = 32 400 que es lo que pagarían de intereses Alberto y su esposa por los 15 años.
al finalizar los 15 años el total a pagar sería el Capital Inicial que les prestaron ( 18 000 ) mas los intereses generados ( 32 400), es decir terminaría pagando S/ 50 400.
Otra forma de obtenerlo es multiplicando la tasa de interés por el número de años 12 x15 = 180 % y sacar luego el 180 % de 18 000 es decir (18 000 x180) / 100 = 32 400 el Total a pagar sería el mismo 18 000 + 32 400 = 50 400
AÑOS
|
1
|
2
|
3
|
4
|
5
|
...
|
15
|
total
|
Interés (12%)
|
2 160
|
2 160
|
2 160
|
2 160
|
2 160
|
2160
|
32 400
|
|
Capital Inicial
|
18 000
|
|||||||
Capital Final (Monto)
|
50 400
|
|||||||
viernes, 24 de abril de 2015
MATEMÁTICA FINANCIERA PARA ADOLESCENTES
Estoy asistiendo a un curso en el cual he obtenido ésta información que comparto hoy con Uds.
La importancia de la Matemática Financiera es cada vez mayor entre los jóvenes; pues ahora ellos se enfrentan con asuntos financieros inmediatos, como por ejemplo cuando deciden sobre un servicio pre pago o postpago de un celular , por lo cual deben familiarizarse con el uso financiero de las matemáticas deben tener conocimientos que le permitan tomar decisiones basadas en ahorro, inversiones que pueden tener características de ser seguras o de riesgo.
Por ejemplo, este dinero depositado (capital) será trabajado por la mencionada entidad y parte del dinero generado con él será “pagado” al dueño del depósito, en este caso, tú.
En cambio, si solicitas un préstamo bancario (capital) a cualquier entidad financiera, le tendrás que pagar intereses a ella.
“Matemática financiera” se refiere a las matemáticas
que se utilizan en el contexto de negocios, finanzas y
economías.
Un componente importante es el interés,
que podría definirse como “el costo del dinero”, y otro
es el capital, dinero que se pone en ahorros o que es
solicitado como préstamo.
Si depositas dinero (capital) en una cuenta de ahorros,
la entidad financiera (banco, caja, etc.) te pagará
intereses por ese depósito.
Para tener éxito con la matemática financiera
Es necesario que los jóvenes conozcan el concepto de porcentajes para poder resolver fórmulas de interés y de inflación. es importante
poseer una base bastante sólida en la resolución de
porcentajes; pues los utilizamos para deducir las tasas de interés de depósitos o préstamos
Por lo tanto, es importante recordar que:
Usamos el símbolo % que se lee “por ciento” para
representar un porcentaje.
Porcentaje es una manera de expresar un número como una fracción del número
100.
Los porcentajes se pueden expresar como decimales.
Un porcentaje expresado como decimal se denomina “tanto por uno”:
1 % = 1/100 = 0,01
10 % = 10/100 = 0,10
P % = p/100
Si queremos emplear fracciones, tienen que estar en su mínima expresión; es decir como fracción irreductible. Por ejemplo,
si hablamos de una mitad, se pueden escribir sus equivalencias:
como fracción 1/2 se lee " un medio"
como decimal 0,5 se lee " cero coma cinco" o " cinco décimos"
como porcentaje 50 % se lee "cincuenta por ciento"
miércoles, 22 de abril de 2015
DIFERENCIAS ENTRE INTERÉS SIMPLE E INTERÉS COMPUESTO
Diferencias entre Interés
Simple e Interés Compuesto
Un punto muy importante y que es realmente básico para hacer crecer nuestros ahorros y no pagar más intereses de la cuenta en
caso de pedir un crédito, es conocer la diferencia entre el interés simple y el interés compuesto.
Mucha gente cree que todas las tasas de interés son
básicamente las mismas, que las disparidades son inapreciables. El caso es que
son bastante diferentes y conocer y entender estas singularidades puede marcar
una gran diferencia en la cantidad de dinero que puedes llegar a ahorrar y a conseguir en tus inversiones.
 Cómo funciona el Interés Simple
Cómo funciona el Interés Simple
La mayoría de la gente cree que todas las tasas de interés funcionan
como el interés simple.
El interés simple funciona de la siguiente forma. Si tienes 1 000 soles y los
metes en un depósito al 5,00% de interés el resultado es de 50 soles.
Es lo
que se nos enseña en el colegio y lo que esta arraigado en nuestra mente. Sin embargo
no es el método que la mayoría de empresas utilizan en el cálculo de los
intereses.
Si crees que todos los tipos de interés trabajan como el interés
simple vas a perder mucho dinero.
Entonces ¿qué otras formas existen para calcular el
interés? Muchas empresas, como bancos y compañías de tarjetas de crédito usan
el interés compuesto para calcular los intereses totales.
Esta forma de calcular los intereses es muy
beneficiosa para estas empresas y bastante menos para los consumidores.
La mayoría de las empresas realizan para un interés
compuesto y además compuesto de forma mensual.
Cómo Funciona el Interés
Compuesto
Veamos un ejemplo. Como antes si tenemos 1 000 soles
al 5,00% de interés. Con el interés simple vimos que el total de intereses es
de 50 soles al final del año.
Pero si usamos
el interés compuesto el cálculo es un poco más complicado, ya que tenemos que
calcular el saldo al final de cada mes.
Empezamos con 1.000 soles al inicio del primer mes,
con un 5,00% de interés. Al final del primer mes se habrán ganado 1/12 de los
intereses que debes ganar en el año. Es decir, 1/12 parte de 50 soles.
Aproximadamente 4,17 soles.
Para el siguiente mes, sumamos esta cantidad a los
1.000 soles, quedando un saldo inicial de 1 004,17 soles.
Repetimos esta operación cada mes (durante el segundo
mes, lo que ganas es 1/12 parte de 1.004,17 soles, etc.), así hasta el último
mes ( mes 12)
Al final del año tendremos 1.000 soles de capital y
51,16 soles de intereses. Comparando tenemos 1,16 soles más de beneficio que si
hubiéramos usado el interés simple.
Si aumentas el capital o el tipo de interés, la diferencia entre
interés simple y el interés compuesto es aún mayor.
Qué Pasa si Pides un
Crédito
Si estas pidiendo un préstamo, usando una tarjeta de crédito por ejemplo, de
3 000 soles con un tipo de interés del 25%.
En principio puede parecer que tienes que pagar unos
intereses al final del año de 750 soles pero esto no es así. Con el interés
compuesto debes un total de 3.850 soles, 100 soles más que con el interés
simple.
Qué Pasa si Ahorras en un
Depósito
Por otra parte, si estás ahorrando dinero veamos que
ocurre. Si tienes 5.000 soles en un depósito al 5,00% de interés al final del
año tendrás 5.250 soles aproximadamente.
Las cantidades resultantes en cada ejemplo son
aproximadas y no se ha tenido en cuenta el cálculo de impuestos y otros gastos
que cobran las empresas financieras para no complicar en exceso los ejemplos.
Lo importante es que entiendas la diferencia entre ambos tipos de interés,
tanto a la hora de ahorrar como de pedir un crédito.
http://www.proahorro.com/
DONDE DEPOSITAR MI DINERO ( AHORRO-CTS) DONDE PRESTAR DINERO
En algunas oportunidades las personas tienen mayores gastos, puede ser por la llegada de las fiestas lo que es un pretexto para comprar bienes más caros. Y necesitan pedir un préstamo, pero antes de hacerlo usted tiene que tener en cuenta esta información.
Al pedir un préstamo, un dato indispensable para elegir la entidad financiera es la tasa de interés que ofrece. Por ello, usted debe conocer qué es la TEA y la TCEA.
La TEA, que la utilizan los bancos, es la tasa efectiva anual; y la TCEA es la tasa de costo efectivo anual.
Así, la TEA es la tasa por el dinero que la entidad financiera le va a prestar, pero, además de esa tasa, la empresa le va a cobrar gastos adicionales, como comisiones. Si incluye estos gastos adicionales en la tasa, entonces usted tendrá la TCEA.
Debe saber también que el interés que Ud, deja de pagar en un mes va a formar parte del capital, es decir se reinvierte, por lo cual Ud. terminará pagando mucho mas de lo que imagina.
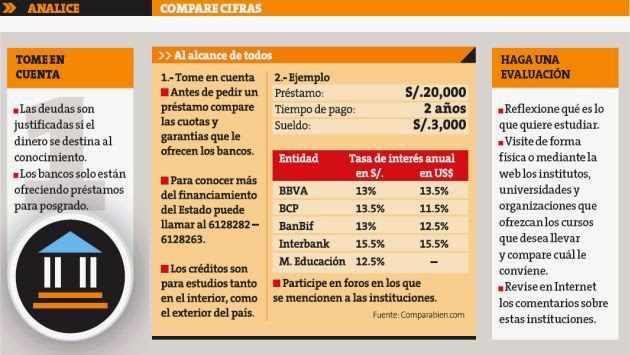
A continuación le presentamos una información con la cual Ud. podrá calcular lo que terminará pagando si solicita un préstamo. Solo tiene que escoger la entidad bancaria, fijarse en la tasa de interés que cobra, poner el monto de capital que va a solicitar y el tiempo que va a demorar en pagarlo
Observe las tasas de Interés y compárelas con las que ofrecen las entidades financieras para el depósito ( Ahorro) y aún para las CTS los siguientes dos cuadros te presentan información de ambos, trabaja de igual manera que como te indiqué para los préstamos y obtendrás cuanto recibirás por tu dinero depositado
Mas o menos así debe ser la caratula de tu tríptico
lunes, 20 de abril de 2015
domingo, 12 de abril de 2015
COMPARACIÓN DE FRACCIONES
Comparar dos fracciones es saber cuál es mayor y cuál es menor. Hay dos maneras fáciles de comparar fracciones: usar decimales, o poner el mismo denominador.
El método decimal de comparar fracciones
Sólo tienes que convertir cada fracción en decimal, y comparar los decimales.
¿Cuál es mayor: 3/8 o 5/12 ?
Hay que convertir cada fracción en decimal. Esto lo puedes hacer dividiendo el numerador entre el denominador (3÷8 y 5÷12), y obtendrás:
3/8 = 0.375, y 5/12 = 0.4166...comparamos los decimales (recuerda que se comparan primero la parte entera y luego la parte decimal empezando de izquierda a derecha décimo con décimo; centésimo con centésimo y asi sucesivamente)
Así que 5/12 es mayor.
El método del mismo denominador
Cuando dos fracciones tienen el mismo denominador (el número de abajo); es decir son homogéneas entonces es fácil compararlas; pues se comparan los numeradores
ejemplo
4/9 < 5/9 (porque 4 es menor que 5)
Pero si las fracciones son heterogéneas (los denominadores no son iguales) debes hacerlas homogéneas (usando Fracciones equivalentes).
Ejemplo:
¿Cuál es mayor: 3/8 o 5/12 ?
Recuerda que para obtener fracciones equivalentes mltiplicas tanto numerador y denominador por un mismo número, entonces, si multiplicas el denominador de la primera fracción 8 × 3 tienes 24, y si multiplicas el de la segunda fracción 12 × 2 también tienes 24, así que hagamos lo mismo con los numeradores:
| y |
| ||||||||||||||||||||||||||||||||||||||
así que con las fracciones homogéneas ( denominadores iguales) vemos fácilmente que 10/24 es mayor que 9/24, por tanto 5/12 es mayor.
Pero cómo poner el mismo denominador
Debemos encontrar el Mínimo común Múltiplo de los denominadores. En el ejemplo anterior, el mínimo común múltiplo de 8 y 12 era 24.y luego para hallar los nuevos numeradores solo divides el mínimo común múltiplo entre el denominador y lo multiplicas por el numerador
| y |
| |||||||||||||||||||||||||||||||||||||
Ejemplo: ¿Cuál es mayor: 5/6 o 13/15?
El mínimo común múltiplo de 6 y 15 es 30. Así que multipliquemos para hacer cada denominador igual a 30:
| y |
| ||||||||||||||||||||||||||||||||||||||
Ahora comparamos 25/30 y 26/30
fácilmente observamos 26/30 > 25/30,
por lo tanto 13/15 es la fracción mayor
OPERACIONES CON FRACCIONES
Ahora recordaremos las operaciones con fracciones como son Suma, resta , multiplicación y división, éste es un tema que has visto desde tus primeros años de estudio. Recuerda que para sumar y restar hay dos formas de hacerlo, teniendo en cuenta que las fracciones tengan o no tengan denominadores iguales; es decir sean homogéneas o heterogéneas pero para la multiplicación y división es lo mismo que sean o no fracciones homogéneas Observa el vídeo y quizá tengas una forma mas fácil de realizar las operaciones.
Ahora observa la representación de las operaciones de fracciones
Ahora observa la representación de las operaciones de fracciones
viernes, 10 de abril de 2015
PORCENTAJES: Descuentos Y Aumentos Sucesivos
Despues de haber visto el video, contesta ¿Cuál era el precio del artículo sin los descuentos?
martes, 7 de abril de 2015
PORCENTAJES - Descuentos Sucesivos
Cuando vas a un supermercado o cuando ves cátalogos de productos; te encuentras muchas veces con ofertas las cuales aparecen en porcentajes y ademas te presentan descuentos adicionales como el de la imagen.Sabemos que tenemos descuentos, que vamos a pagar menos, pero ....¿sabemos obtener exactamente cuànto vamos a pagar?
Pues eso es lo que vamos a ver hoy con DESCUENTOS SUCESIVOS.
Vamos a trabajar con el afiche que tenemos a la vista; por el día del Padre, vamos a comprarle un par de zapatos, su precio es S/ 280, según el afiche tiene un descuento del 30 % y como contamos con tarjeta Metro, tenemos además un descuento adicional del 5 %.¿Cuánto pagaremos por el par de zapatos para papá?
Primero sacaremos el 30 % de S/ 280 que viene a ser S/ 84, y restamos éste resultado de los 280 que era su precio sin descuento, obtenemos S/ 196 a éstos S/ 196 recien le sacamos el 5 % ( descuento adicional por tener tarjeta metro); 0btenemos S/ 9,80, restamos nuevamente de los 196 y obtenemos S/ 186,20 que es lo que vamos apagar por el par de zapatos para papá.
30 % de 280 sabiendo que el 10% de 280 es 28 entonces el 30 % será 28 x 3 = 84
Restamos 280- 84 = 196
el 5 % de 196 es 9,80 sabemos que el 10 % es 19,6 entoces el 5 % será 19,6 : 2 = 9,80
Restamos
196 - 9,80 = 186,20
Si sumamos los 2 descuentos ofrecidos, piensas que pagaríamos lo mismo;....No! no es lo mismo; vamos a ver un video en donde se te muestra como obtienes el descuento único, en descuentos sucesivos
PORCENTAJES: Aumento Sucesivo
En el mundo laboral es mas común ver los aumentos sucesivos, por ejemplo en el pago de horas extras o en el incremento de sueldos.
Vamos a trabajar con un ejemplo para que sea mas fácil.
El Sr. Ramos trabaja como administrador en un supermercado, su sueldo por hora es de S/120 y por cada hora adicional le aumentan 10% del monto anterior. si trabajó 2 horas adicionales ¿Cuánto recibirá al final del día?
si el sueldo por hora es S/ 120 el 10 % serán S/ 12 por lo tanto recibirá S/ 132
(120 + 12 = 132) pero no trabajó solo una hora sino 2 horas adicionales, entonces volvemos a sacar el 10% que le pagan por hora adicional.
el 10 % de 132 es 13,20 entonces recibirá S/ 145,20 ( 132 + 13,20 ).
Otra forma en que te presenten el problema es solicitándote el aumento único que ha recibido el Sr. Ramos, viendo el siguiente vídeo podrías hallar la respuesta
domingo, 5 de abril de 2015
MI PESO IDEAL
“EL PESO IDEAL PARA LOS ADOLESCENTES”
El peso ideal para los adolescentes depende en gran medida de su índice de masa corporal o IMC. Este cálculo determina la salud del adolescente basándose en su actual altura, peso, edad y género.
Los adolescentes que caen en el percentil 50 de la tabla de IMC se consideran peso medio, que es el
ideal para estar sano, pero el adolescente no debe entrar en pánico si cae por debajo del peso promedio o superior al promedio
en peso. Según publicaciones de organizaciones de salud, la pubertad hace que
el peso del cuerpo de adolescente fluctúe debido a los cambios hormonales en el
cuerpo.
-
Pero, ¿cómo calcular el índice de masa corporal del adolescente para determinar un peso saludable basada en la edad y el género? A continuación, se explica:
- Anotar en un diario el peso del adolescente para registrar los cambios en el tiempo.
- Pídale al adolescente ponerse de pie contra una pared y colocar el extremo metálico de la cinta métrica en el suelo. Coloque la cinta métrica en la pared y marque el punto directamente sobre la cabeza del adolescente para determinar su altura.
- Multiplique la altura del adolescente (en metros) al cuadrado. Luego, pese al adolescente (en kilogramos) y divida este número entre su altura al cuadrado. El resultado representa el índice de masa corporal según el Adolphe Quetelet (1796-1874).
| Indice de Masa Corporal (IMC) | Clasificación |
| Menor a 18 | Peso bajo. Necesario valorar signos de desnutrición |
| 18 a 24.9 | Normal |
| 25 a 26.9 | Sobrepeso |
| Mayor a 27 | Obesidad |
| 27 a 29.9 | Obesidad grado I. Riesgo relativo alto para desarrollar enfermedades cardiovasculares |
| 30 a 39.9 | Obesidad grado II. Riesgo relativo muy alto para el desarrollo de enfermedades cardiovasculares |
| Mayor a 40 | Obesidad grado III Extrema o Mórbida. Riesgo relativo extremadamente alto para el desarrollo de enfermedades cardiovasculares |

Por ejemplo, un hombre o una mujer que pesa 120 kilos y mide 1.65 metros, tiene el IMC igual a 44,
Peso = 120 kg = 120 kg = 44
Estatura² 1.65 x 1.65 2.7225
es decir, Obesidad Mórbida o Extrema, con un riesgo relativo muy alto para el desarrollo de enfermedades cardiovasculares.
Recuerde que si el adolescente tiene sobrepeso, en esta etapa puede perder peso con simplemente hacer más actividad física.
Ahora que has aprendido a obtener tu Indice de masa corporal habrás notado que has utilizado matemática para obtenerlo; haciendo uso de las operaciones con números racionales, asi también podras obtener las equivalencias de los números decimales y las fracciones espero no tengas dificultad alguna.
Suscribirse a:
Comentarios (Atom)